6th Class Session

Sixth Class Session

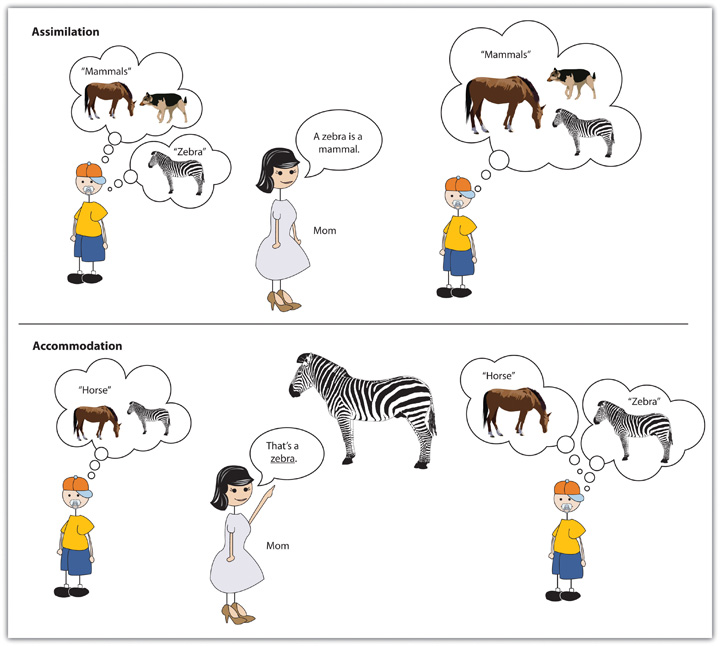
In this last session, we learned about differentiated instructions and assessment.


abstracted from http://www.differentiatedkindergarten.com/2012/08/is-on-going-assessment-driving-your.html


Dr Yeap told us that there are four questions to ask ourself when we plan a lesson.

1. What do I want the students to learn?
    - Focus on learning and not teaching.

2. How do I know that they have learned?
   - Assessing children if they are able to articulate the process of working out the problem
  
3. What if they can't?
    - Teacher will have to revisit the topic again with concrete materials by scaffolding.

4. What if they already can?
    - Provide enrichment to challenge the advance learner while others are still working on the problem
    (*Reminder: not to teach ahead!).


Teaching process
1. Show (modelling)
2. Scaffolding
3. Children work on their own

We also worked on graph. Dr Yeap mentioned that we should do human graph with the children we are teaching at this level. If we are representing a person in the graph, we should avoid using general ones like shapes/colours, instead we should use picture of a person. 

Human bar graph

     
abstracted from http://www.walterstownns.ie/travel.html

5th Class Session

Fifth Class Session

In this session, Dr Yeap spoke about Dienes's theory on perceptual variability principle.

Perceptual Variability or Multiple Embodiment Principle: In order to allow as much scope as possible for individual variations in concept-formation and to induce children to gather the mathematical essence of an abstraction, the same conceptual structure should be presented in the form of as many perceptual equivalents as possible.

(Adapted from Dienes, Z.P, 1971 Building up Mathematics,4th ed.)

Also, for younger children, it is better to provide them with proportionate materials to manipulate with rather than non-proportionate materials. In addition, the materials must be natural, for instance when we teach children counting, we use eggs, then later move on to unnatural materials such as teddy bear counters.

            to      

In order to help children learn maths, teachers have to

1. Provide opportunities for children to count, sort/classify and match to develop number sense.

abstracted from http://snoqualmievalley.macaronikid.com/article/101947/national-trimathlon-at-mathnasium-of-issaquah

 

2. Provide opportunities for children to work with patterns - number patterns, colour patterns, shape patterns.

   

3. Provide opportunities for children to develop visualisation skills - concrete experiences, playing with lego blocks, movement activities and drawing. 

 

abstracted from
http://learningspecialistmaterials.blogspot.sg/2012/08/the-ten-visualization-skills-needed-to.html

4. Provide opportunities for children to communicate - talk and listen to how others solve a problem (children will learn new strategies when talking to one another)

When do we teach shapes to children?

I guess most of our answers would be in nursery (4 years old). Surprise, surprise, surprise! It should be taught in K2 (6 years old) and only the names of the shapes should be taught. Our group (Fiona, Dawn and I) got to know this when we asked him about our group assignment. We were very surprised by it as we introduced shapes to the children when they are in nursery. Most of the children came to us with the prior knowledge of identifying and naming shapes. The question of the day - "Are we over teaching the children?"

4th Class Session

Fourth Class Session

In this session, we discussed the idea of assimilation and accommodation by Jean Piaget.


abstracted from http://www.simplypsychology.org/piaget.html#sthash.2LeVKM5T.dpbs

Assimilation: When a child responds to a new event in a way that is consistent with an existing schema.
Accommodation: When a child modifies an existing schema or forms an entirely new schema to deal with a new object or event.
Example:

abstracted from http://catalog.flatworldknowledge.com/bookhub/reader/127?e=stangor-ch06_s02


Implications: Adults/teachers must not spoon feed children to make their life easier. They will not have enough schema in their brains. If children only assimilate but don't accommodate, the schema will not be refined, or new schema will not be formed. 


We also manipulated with tangrams to find out which are the shapes that could be combined to form a similar but larger shape.

 

Just want to share this which I thought is rather cute.

 
abstracted from  http://alyon.weebly.com/2/archives/09-2011/1.html 

3rd Class Session

Third Class Session

In this session, we learned about fractions. Truth be told, I was not good in solving fraction problems as I am bad at visualising. This class session refreshed my memory of learning fractions in primary school. We were each given a piece of paper and we were asked to fold that into four equal parts. It's interesting to know that amongst our coursemates, we have different ways of folding that piece of paper. It shows that there is no one way to solve a math problem. Each of us have different ways of looking into a problem and thus having different ways to solve it. Similarly, it applies to the children too.

These diagrams could help you to have a better understanding about fractions.

abstracted from http://www.freewebs.com/workstattion/MATH/fractions/activities.htm


abstracted from http://manicmathmadness.blogspot.sg/2010/09/fractions-level-4.html

Dr Yeap has been emphasizing on CPA approach when teaching children in his sessions.
Concrete > Pictorial > Abstract approach enables students to encounter math in a meaningful way and translate mathematical skills from the concrete to the abstract.


abstracted from http://www.aspacio.net/2012/10/the-2nd-singapore-math-learning.html

For instance, when introducing fractions to children, allow them to explore with concrete materials first - folding a piece of paper into four equal parts. Then, checking for equal parts by overlapping. If the parts are divided into different shapes, cut them out and rearrange them to see if they overlap one another nicely.
Children will then constructed the idea of equal parts = equal amount. Thereafter, they could solve problems using the pictorial form of the shapes. Finally, they could solve problems of abstract symbols e.g. 1/4 + 3/4.

Check out this link, it has lessons and practice games pertaining to fractions.
http://www.coolmath4kids.com/fractions/index.html

2nd Class Session

Second Class Session

In the second class session, Dr Yeap mentioned about a point that I agreed strongly. That is teachers could give information to children but they could not give knowledge to them. Knowledge have to be constructed by learners themselves. Our role as teachers is to help children to relate/make connections to new ideas to what they have already understand (prior knowledge).


Problem: How many paper clips?
From this problem that we solved in class, I have learned that when we want children to do a comparison, for instance how many paper clips were in each bottle, we have to provide them with a benchmark (3 paper clips). Then they would come up with strategies on how to find out the number of paper clips in each bottle - by listening to the sound when each bottle is shaked.

Dr Yeap reminded us that shapes cannot be compared using big/small, we can only compare "which is bigger or smaller", for e.g. triangle A is smaller than triangle B. It made me realised that most of the time, we often use the wrong 'term' when we explain or ask questions to children. For instance, "which triangle is big and which triangle is small".  So, from today onwards, I will have to remind myself to use the correct term and the right language when I am teaching the children.




How many spoons are there altogether?

There are 5 spoons altogether. - How do I know? 

1. By counting to one-to-one correspondence

2. By subitizing (looking) - One new word that I learned from Dr Yeap :)

1st Class Session

EDU 330: Elementary Mathematics

First Class Session

In class today, we learned about the uses of numbers and I have learned 2 new terms - rational numbers and nominal numbers. We had been using the latter in our daily lives such as our I/C numbers, phone numbers, bus numbers and etc. It's just that most of us didn't know the name of it.

nominal numbers: numerals with no information other than identification purpose (name)

   



 

 

rational numbers: any numbers that can be expressed as a fraction